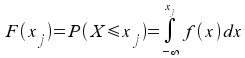Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken

3. Eigenschaften und Verteilungen einer stetigen Zufallsvariablen

Im Gegensatz zu diskreten Zufallsvariablen haben stetige Zufallsvariablen unendlich viele Realisationsmöglichkeiten. Betrachtet man beispielsweise die Körpergröße von Personen in einer Stichprobe, so ist offensichtlich, dass ihr Wertebereich unendlich viele Elemente umfasst, da es sowohl zwischen 185 cm und 186 cm als auch zwischen 185,536 cm und 185,537 cm immer noch unendlich viele mögliche Ausprägungen gibt. Eine empirische Grenze wird hier lediglich durch die Genauigkeit des verwendeten Messinstrumentes gesetzt.

Dies bedeutet gleichzeitig, dass der Wert der Wahrscheinlichkeitsfunktion f(x_j) für eine konkrete Ausprägung x_j Null wäre, ohne jedoch ein unmögliches Ereignis zu sein¹. Aus diesem Grunde muss der Funktion f(x_j) eine andere Bedeutung gegeben werden.

a) Das Konzept der Wahrscheinlichkeitsdichte

Der Begriff der Wahrscheinlichkeitsdichte ist, analog zum Begriff der Häufigkeitsdichte aus der deskriptiven Statistik, zu verstehen als Realisation einer Variablen in einem Werte-Bereich.

• f(x_j) wird demnach für stetige Zufallsvariablen als Wahrscheinlichkeitsdichte bezeichnet.
  
  f(x_j) gibt dabei nicht die Wahrscheinlichkeit für ein konkretes x, sondern die Wahrscheinlichkeit für einen Bereich um x mit einer definierten Unter- und/oder Obergrenze an.

• Es gilt: f(x_j) ≥ 0 , d.h. die Wahrscheinlichkeitsdichte ist nicht mehr nach oben auf den Wert von Eins begrenzt.

b) Die (Wahrscheinlichkeits-)Dichtefunktion

• Die Dichtefunktion ist eine manchmal lineare, wie wir im nächsten Abschnitt sehen werden, meist aber eine nichtlineare Funktion:
  f(x_j) = g(X)

  • Beispiel einer linearen Dichtefunktion ist die für den Wertebereich 0 ≤ x_j ≤ 2 definierte Funktion f(x_j) = 0,5 x (vgl. Abb. I-8a),

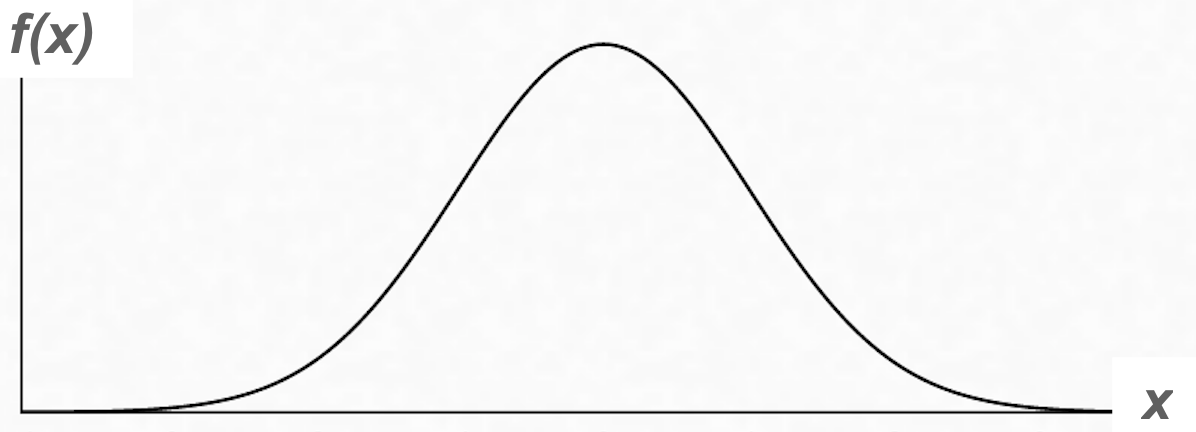
  • Beispiel für eine nichtlineare Funktion ist die, in der induktiven Statistik zentrale, deshalb im nächsten Kapitel ausführlich diskuierte Standardnormalverteilung (vgl. Abb. I-9)

• Graphisch ergibt sich die Dichtefunktion als stetiger linearer oder nichtlinearer Kurvenzug, mit im Definitionsbereich positiven Ordinatenwerten. Als einfaches Beispiel wird im Folgenden eine lineare Funktion und die nichtlineare, symmetrische Standardnormalverteilung Verteilung präsentiert:

  • Abbildung I-9: Stetige (lineare) Dichtefunktion

    .

  • Abbildung I-10: Stetige (symmetrische) Dichtefunktion

    

• Für stetige Zufallsvariablen gilt (wie auch für die diskreten), dass die Gesamtheit ihrer Elementarereignisse das sichere Ereignis ausmachen. Für stetige Zufallsvariablen wird dies als Integral über den gesamten Wertebereich ausgedrückt, das den Wert 1 hat:

  .

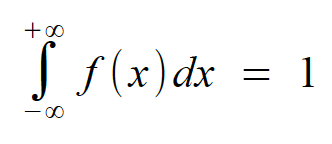  In den Graphiken bedeutet dies, dass die Fläche unter der Dichtefunktion im Definitionsbereich gleich Eins ist (wie man in Abb. I-9 unmittelbar sieht).

• Bei der Bestimmung der Wahrscheinlichkeit, dass eine stetige Zufallsvariable in einem bestimmten Bereich liegt, ist es unerheblich, ob die Grenzen a und b mit einbezogen werden oder nicht. Weil, wie gesehen, die Wahrscheinlichkeit für konkrete Einzelwerte Null ist, kann
  

  P( a ≤ X ≤ b ) = P( a < X < b )

  gesetzt werden.

c) Die Parameter der Dichtefunktion

Die Berechnung von Erwartungswert und Varianz erfolgt ähnlich wie im Falle diskreter Zufallsvariablen, aber wieder unter Verwendung des Integrals:

• Der Erwartungswert einer stetigen Zufallsvariablen ergibt sich als:

  

• Die Varianz einer stetigen Zufallsvariablen ist:

  

d) Die Verteilungsfunktion

Die Verteilungsfunktion ist ebenfalls als bestimmtes Integral definiert:

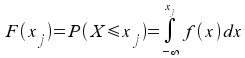
Sie ist graphisch als Fläche unter der Dichtefunktion implizit darzustellen oder über ihre explizite Funktion, für die nachfolgend nochmals auf das Beispiel einer Normalverteilung zurückgegriffen wird:

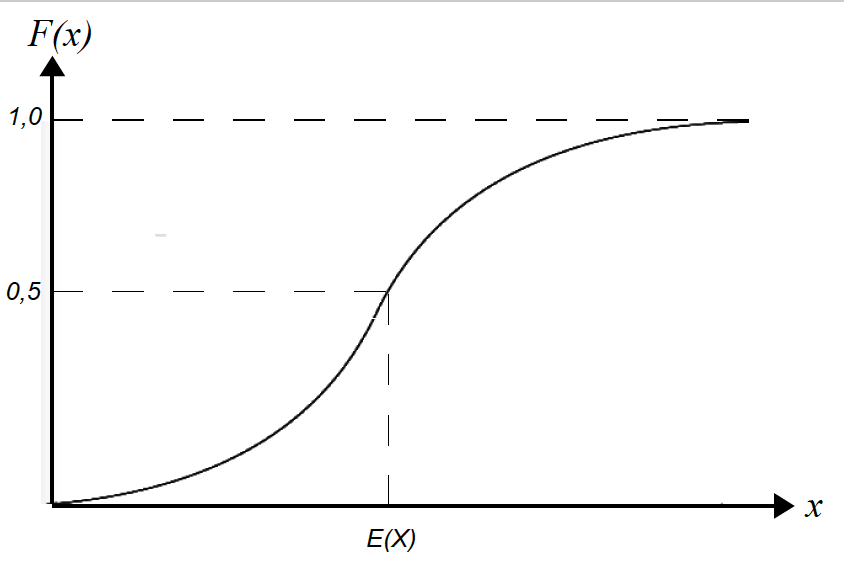
Abbildung I-11: Verteilungsfunktion einer stetigen (symmetrischen) Zufallsvariablen

letzte Änderung am 5.4.2019 um 4:24 Uhr.

Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles2/kapitel01_Grundlagen~~lder~~l~~lWahrscheinlichkeitsrechnung/modul04_Zufallsvariablen~~lund~~lihre~~lVerteilung/eben
e01_Konzepte~~lund~~lDefinitionen/01__04__01__02.php3
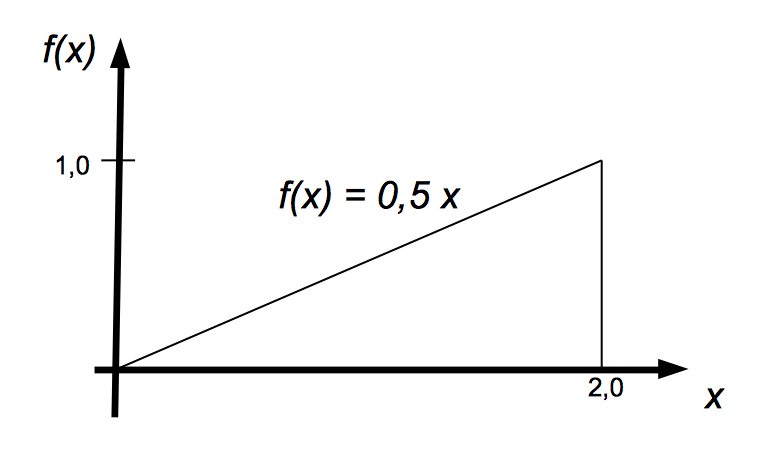
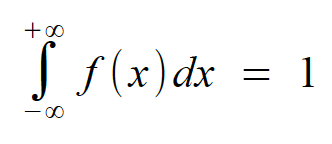