| Druckversion: | | Nach dem Drucken: | | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
Konzepte und Definitionen im Modul II-4 Die t-Verteilung
1. Vorbemerkungen
Die t-Verteilung wurde 1908 von Gosset unter dem
Pseudonym „Student“ eingeführt. Sie ist daher bis
heute auch unter der Bezeichnung „Student-Verteilung“
bekannt.
Die (Student-) t-Verteilung dient in der induktiven
Statistik als Basis der Verteilung von Stichprobenmittelwerten aus
kleinen Stichproben
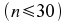 und
ist somit Grundlage der statistischen Schlüsse auf den
entsprechenden Parameter.
und
ist somit Grundlage der statistischen Schlüsse auf den
entsprechenden Parameter.
2. Die t-Verteilung und ihre Eigenschaften
a) Die Dichtefunktion
b) Parameter und Maßzahlen der Dichtefunktion
Der einzige Parameter der Dichtefunktion ist die Anzahl der Freiheitsgrade
 .
.
Der
Erwartungswert der t-Verteilung ist erst ab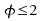 gegeben
und beträgt dann:
gegeben
und beträgt dann:
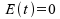 .
.
Die Varianz der t-Verteilung kann
ab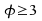 berechnet
werden und beträgt:
berechnet
werden und beträgt:
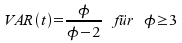
c) Die graphische Darstellung der Dichtefunktion
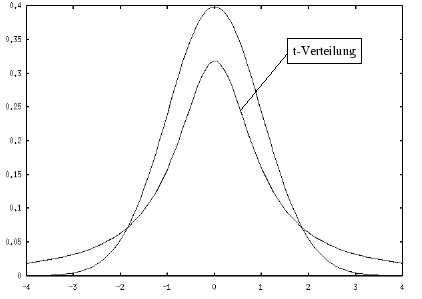
Der Graph der t-Verteilung ist um symmetrisch
und ähnelt mit seiner Glockenform der
Normalverteilung, allerdings verläuft er flacher als diese:
symmetrisch
und ähnelt mit seiner Glockenform der
Normalverteilung, allerdings verläuft er flacher als diese:
Abbildung II-13: Vergleich der Standardnormalverteilung mit einer
Student t-Verteilung mit

d) Die tabellierte Verteilungsfunktion
Die Randwahrscheinlichkeiten der
t-Verteilung für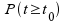 liegen
ebenfalls in tabellierter Form vor. Ein Auszug für findet sich
in Tab. II-6:
liegen
ebenfalls in tabellierter Form vor. Ein Auszug für findet sich
in Tab. II-6:
Tabelle II-6: Randwahrscheinlichkeiten der t –
Verteilung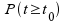 für
für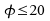

In der Tabelle sind die
Freiheitsgrade in der Vorspalte zu finden, die kritischen Werte
für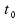 im
inneren der Tabelle und die korrespondierenden
Rand-Wahrscheinlichkeiten in den Spaltenüberschriften. Eine detaillierte Tabelle findet
sich hier.
im
inneren der Tabelle und die korrespondierenden
Rand-Wahrscheinlichkeiten in den Spaltenüberschriften. Eine detaillierte Tabelle findet
sich hier.
e) Die Approximation durch die Standard-Normalverteilung
Ab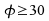 ist
die t-Verteilung hinreichend genau durch die Standardnormalverteilung
approximierbar. Es gilt dann:
ist
die t-Verteilung hinreichend genau durch die Standardnormalverteilung
approximierbar. Es gilt dann:

letzte Änderung am 5.4.2019 um 4:24 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles2/kapitel02_Theoretische~~lVerteilungen/modul04_t-Verteilung/ebene01_Konzepte~~lund~~lDefinitionen/02__04__01__01.php
3
![]() und
ist somit Grundlage der statistischen Schlüsse auf den
entsprechenden Parameter.
und
ist somit Grundlage der statistischen Schlüsse auf den
entsprechenden Parameter.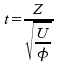 mit
mit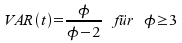


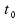 im
inneren der Tabelle und die korrespondierenden
Rand-Wahrscheinlichkeiten in den Spaltenüberschriften. Eine detaillierte Tabelle findet
im
inneren der Tabelle und die korrespondierenden
Rand-Wahrscheinlichkeiten in den Spaltenüberschriften. Eine detaillierte Tabelle findet