1. Definitionen der Wahrscheinlichkeit

Die Wahrscheinlichkeit des Ereignisse A wird mit P(A) bezeichnet. Sie ist ein Zahlenwert, mit dem die Realisationschance dieses bestimmten Ereignisses quantifiziert wird. Es gibt dazu verschiedene Ansätze zur konkreten Bestimmung seines Wertes und ein Axiomensystem zum Rechnen mit diesen Werten.

a) Die klassische objektive Wahrscheinlichkeit

Nach dem Konzept der klassischen objektiven Wahrscheinlichkeitt werden mit P(A) die Anzahl der, dem Ereignis A zuzurechnenden Elementarereignisse [= n(A)] ins Verhältnis zur Anzahl aller Elementarereignisse [= n(E)] gesetzt:

So ergibt sich die Wahrscheinlichkeit eine gerade Zahl zu würfeln aus dem Verhältnis der günstigen Ereignisse (=3) zu den möglichen Ereignissen (=6) mit P(A) = 3/6 = 0,5.
Ist die Durchführungsvorschrift des Zufallsexperimentes bekannt, so kann nach dieser Definition die Wahrscheinlichkeit jedes möglichen Ergebnisses bereits ermittelt werden, bevor das Experiment tatsächlich ausgeführt wird. Aus diesem Grunde wird die klassische objektive Wahrscheinlichkeit nach Laplace auch als a-priori-Wahrscheinlichkeit bezeichnet.
Es ist jedoch zu beachten, dass bei dieser Definition nach dem Prinzip des unzureichenden Grundes unterstellt wird, dass die Realisation aller Elementarereignisse gleich wahrscheinlich ist. Daher wird z.B. ein „idealer Würfel“, dessen Augenzahlen exakt mit der gleichen Wahrscheinlichkeit von 1/6 fallen, häufig auch als „Laplace-Würfel“ bezeichnet.

Sobald es hinreichenden Grund zu der Annahme gibt, dass für die Elemente des Ereignisraumes eines Zufallsexperimentes ungleiche Eintrittswahrscheinlichkeiten vorliegen, ist das Konzept der klassischen objektiven Wahrscheinlichkeit ungeeignet.

b) Die statistische objektive Wahrscheinlichkeit

Wenn die Elementarereignisse eines Zufallsexperimentes mit ungleicher Wahrscheinlichkeit auftreten, muss die tatsächliche Wahrscheinlichkeit als statistische objektive Wahrscheinlichkeit approximativ empirisch bestimmt werden. Dies gilt z.B. für die Ermittlung der Wahrscheinlichkeit dafür, dass eine Reißzwecke auf den Kopf oder auf die Seite fällt.
Diese statistische objektive Wahrscheinlichkeit ist definiert als Grenzwert der relativen Häufigkeit des Auftretens von A bei wiederholter Durchführung des Experimentes:

Je häufiger das Zufallsexperiment wiederholt wird, desto mehr nähert sich P(A) der tatsächlichen Wahrscheinlichkeit an. Diese Wahrscheinlichkeit wird deshalb auch als a-posteriori-Wahrscheinlichkeit genannt.
Wirft man z.B. eine Münze immer wieder und ermittelt wie oft „Wappen“ im Verhältnis zur Zahl der Würfe gefallen ist, so wird sich die Wahrscheinlichkeit bei einer idealen Münze immer näher bei 0,5 stabilisieren.

In vielen, oft nicht objektivierbaren Kontexten, z. B. bei zukünftigen Ereignissen, über deren Realisierungschancen noch keine Erfahrungswerte vorliegen, also etwa bei der Analyse von Wettkampf- oder von ökonomischen Entscheidungssituationen, sind die bisher entwickelten Ansätze nicht brauchbar. Dazu ist das Konzept der subjektiven Wahrscheinlichkeit entwickelt worden.

c) Die subjektive Wahrscheinlichkeit

Bei dem von Bayes entwickelte Konzept der subjektiven Wahrscheinlichkeit wird die subjektive Wahrscheinlichkeit als zahlenmäßiger Ausdruck der persönlichen Einschätzung der Realisierbarkeit des Ereignisses A gewertet.
Konkret definiert Bayes dazu die Wahrscheinlichkeit des Ereignisses A als Verhältnis des durchschnittlichen zu erwartenden Gewinns und des Gewinns bei Eintreten des Ereignisses.

Geht man davon aus, dass in einer fairen Entscheidungssituation der durchschnittlich zu erwartende Erfolg oder Gewinn dem Einsatz entspricht, kann man dies auch formulieren als

Werden z.B. bei einem Pferderennen 50 € auf den Sieg des Pferdes A gesetzt, wobei beim Sieg von A 150 € Gewinn ausgezahlt würden, ergäbe sich:

Die Einschätzung erfolgt also aus der speziellen Entscheidungssituation heraus, daher der Begriff subjektive Wahrscheinlichkeit.

Nun ist klar ersichtlich, dass die oben skizzierten Definitionen kein Fundament für eine allgemein gültige Wahrscheinlichkeitstheorie liefern können, da sie alle auf bestimmte Problemstellungen abheben und nur im jeweils passenden Kontext Verwendung finden können. Ein übergreifendes Konzept muss also unabhängig von der jeweiligen Problemstellung definiert werden.

d) Die axiomatische Definition der Wahrscheinlichkeit

Dieser Begriff der Wahrscheinlichkeit, der auf Kolmogoroff zurückgehen, stützt sich ausschließlich auf die mathematischen Eigenschaften der Wahrscheinlichkeit und basiert auf folgenden drei Axiomen:

1. Axiom: Die Wahrscheinlichkeit P(A _i ), mit i = (1....n) ist eine eindeutig bestimmte, reelle, positive Zahl zwischen Null und Eins.¹



2. Axiom: Die Wahrscheinlichkeit des sicheren Ereignisses ist Eins:




3. Axiom: Die Wahrscheinlichkeit der Vereinigung disjunkter Ereignisse A _i , mit i = (1....n) ergibt sich als Summe der Wahrscheinlichkeiten der einzelnen Ereignisse (Additionssatz für disjunkte Ereignisse):



oder allgemein:

e) Folgerungen aus der axiomatischen Definition der Wahrscheinlichkeit

Aus diesen drei Axiomen folgt:

• Die Wahrscheinlichkeit des komplementären Ereignisses ist
  

  

• Die Wahrscheinlichkeit der Schnittmenge zweier diskunkter Ereignisse A und B ist Null.
  

  

• Die Wahrscheinlichkeit eines Teilereignisses ist immer kleiner (oder gleich) als die des übergeordneten Ereignisses:

  

• Für nicht disjunkte Ereignisse folgt daraus der Additionssatz für beliebige Ereignisse:

Die Wahrscheinlichkeit des Durchschnitts P(A ∩ B) muss hier subtrahiert werden, da sie sonst doppelt enthalten wäre.

2. Abhängige Ereignisse und bedingte Wahrscheinlichkeiten

a) Die Wahrscheinlichkeiten mehrdimensionaler Ereignisse

Wenn Ereignisse zusammen oder nacheinander auftreten, d.h. im Falle mehrdimensionaler Ereignisse, stellt sich die Frage nach der Abhängigkeit bzw. Unabhängigkeit der Ereignisse. Bei Abhängigkeit ist zu klären, wie sich ihre Wahrscheinlichkeit verändert, wenn bestimmte Bedingungen erfüllt sind.

Klassisches Beispiel dafür ist die Ziehung verschieden markierter Kugeln aus einer Urne, ohne dass die gezogenen Kugeln in die Urne zurück gelegt werden (z.B. Ziehung der Lottozahlen). Bei solchen klassischen Urnenexperimenten ändern sich die Wahrscheinlichkeiten offensichtlich nach jeder Ziehung, da sich sowohl die Zahl der günstigen als auch die Zahl der möglichen Fälle mit jeder entnommenen Kugel verändern.

Stellen wir uns dazu eine Urne vor, die vier rote und sechs grüne Kugeln enthält. Aus dieser Urne werden nun nacheinander zwei Kugeln gezogen und beiseite gelegt (also nicht zurück in die Urne).
Die Wahrscheinlichkeit, im ersten Zug eine rote Kugel zu ziehen, beträgt als Verhältnis der günstigen zu den möglichen Fällen P(A) = 4/10. Es sind danach noch insgesamt 9 Kugeln in der Urne, davon 3 rote, d.h. die Bedingung für den zweiten Zug ist eine andere als die für den ersten Zug.

b) Die bedingte Wahrscheinlichkeit

Die Wahrscheinlichkeit, im zweiten Zug wieder eine rote Kugel zu ziehen, nachdem im ersten bereits eine der roten Kugeln entnommen wurde, liegt nun bei 3/9, d.h. die Wahrscheinlichkeit für "rot im ersten Zug" unterscheidet sich von der Wahrscheinlichkeit für "rot im 2. Zug". Wir nennen diese Wahrscheinlichkeit für den 2. Zug bedingte Wahrscheinlichkeit, weil sie sich unter der Bedingung des 1. Zuges ergibt.

Für die bedingte Wahrscheinlichkeit, dass ein Ereignis B eintritt, nachdem zuvor bereits A eingetreten ist, verwenden wir die Schreibweise

In unserem Beispiel also: P(B | A) = 3/9

c) Der Multiplikationssatz für abhängige Ereignisse

Die Gesamtwahrscheinlichkeit für den Fall „rot im ersten Zug, rot im zweiten Zug“ liegt bei P(A ∩ B) = 4/10 · 3/9 = 0,1333 . Graphisch lässt sich diese Wahrscheinlichkeit in Abb. I-4 als Verhältnis der Kreuze in der grau unterlegten Fläche (12 Kreuze) zu den Kreuzen der Gesamtfläche (90 Kreuze) darstellen.

Abbildung I-4: Urnenexperiment und Ereignisraum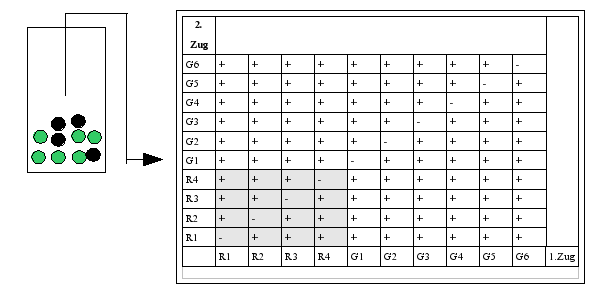

• Allgemein formuliert dies der Multiplikationssatz für abhängige Ereignisse:

  

• Daraus resultiert die Formel für die bedingte Wahrscheinlichkeit:

d) Der Multiplikationssatz für dreidimensionale abhängige Ereignisse

Betrachten wir noch den Fall der Ziehung von drei Kugeln aus obiger Urne, exemplarisch für den Fall „rot, grün, rot“. Hier erhalten wir:
P(A ∩ B ∩ C) = 4/10 · 6/9 · 3/8 = 0,10,

oder allgemein:

3. Unabhängige Ereignisse

Anders liegt der Fall für das obige Experiment, wenn nach der Ziehung jede Kugel sofort wieder in die Urne zurück gelegt wird (Ziehung mit Zurücklegen). In diesem Fall ist die Bedingungg für den zweiten Zug identisch mit der für den ersten Zug, d.h. Ereignisse sind voneinander unabhängig und die bedingten Wahrscheinlichkeiten entsprechen den einfachen Wahrscheinlichkeiten.

Ausgedrückt wird dies durch den Multiplikationssatz für unabhängige Ereignisse:

,

bzw. allgemein für n beliebige Ereignisse:

.

Für den obigen Beispielsfall („rot, rot“) ergibt: P(A ∪ B = 4/10 · 4/10 = 0,16. Auch dieser Fall kann an Abb. I-4 veranschaulicht werden: Im Falle des Zurücklegens wäre die Hauptdiagonale ebenfalls mit Kreuzen besetzt. Die grau unterlegte Fläche würde 16 Kreuze und der gesamte Ereignisraum 100 Kreuze aufweisen.

4. Das Theorem der totalen Wahrscheinlichkeit und der Satz von Bayes

a) Das Theorem der totalen Wahrscheinlichkeit

Sind A _i , (i = 1....n) originär disjunkte Ereignisse mit

so wird die Menge derart definierter Ereignisse A _i , (i = 1....n) . als Einteilung bezeichnet (vgl. Abb. I-5). Das Theorem der totalen Wahrscheinlichkeit bezieht sich nun auf die Wahrscheinlichkeit der Ereignisses B als Summe von Teilereignissen von A _i , (i = 1....n) .

Abbildung I-5: Theorem der totalen Wahrscheinlichkeit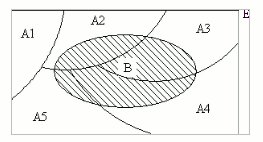

Das Theorem der totalen Wahrscheinlichkeit bestimmt unter obiger Bedingung nun die Wahrscheinlichkeit eines Ereignisses B als Summe der Wahrscheinlichkeiten von sich gegenseitig ausschließenden Ereignissen (A₁ ∪ B):

.

b) Der Satz von Bayes

Aus der der Identität von (B ∩ A) = (A ∩ B und der Formel für bedingte Wahrscheinlichkeiten resultiert:

.

Satz von Bayes bestimmt daraus die a-posteriori-Wahrscheinlichkeit eines Ereignisses A als Ursache des Ereignisses B:

Hinweis zur Navigation, zum Ausdrucken und zur Bewertung: In der Abschusszeile finden Sie einen Link zur Druckversion, zum vorherigen und zum nächsten Arbeitsschritt und mit der Sitemap eine Übersicht über das gesamte Angebot. Zur Bewertung: Diese Seite ist überarbeitet worden. Deshalb wurden die bisherigen Bewertungen gelöscht. Bewerten Sie bitte diese aktualisierte Seite neu und helfen Sie uns, damit dieses Angebot weiter zu verbessern: Diese Seite ist: sehr gut    gut    eher gut    mittelmäßig    eher schlecht    schlecht    sehr schlecht Diese Seite wurde von 3 Benutzern im Durchschnitt mit "gut" bewertet.

1/2 50 % Fortschritt

| Feedback | Copyright | Übersicht | Druckversion | Log-Out | Sitemap | Nächster Arbeitsschritt |